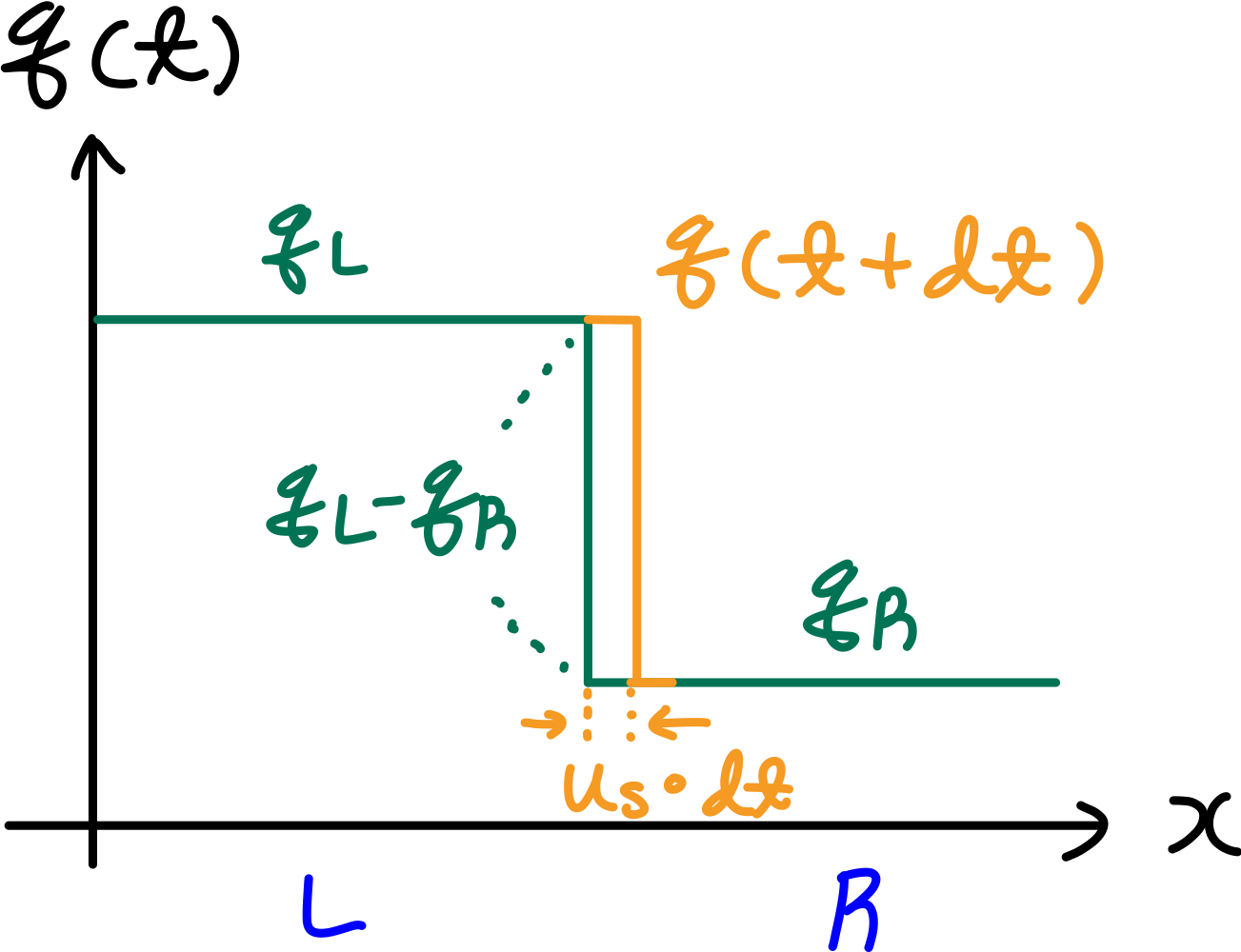
Shock Speed Derivation
충격파(shock wave)는 쌍곡형 보존 법칙(hyperbolic conservation law)의 해가 불연속성을 가질 때 발생하는 급격한 전파 현상입니다. 이 글에서는 임의의 보존량 $q$에 대한 1차원 보존 법칙
\[\partial_t q + \partial_x f(q)=0 , \qquad x \in \mathbb{R}, \; t>0\]에서 충격파 전파 속도(shock speed) $u_s$를 엄밀하게 유도하고, $q$의 불연속 크기가 작아질 때 이 속도가 특성 속도(characteristic speed) $c=\frac{df}{dq}$로 수렴함을 보이겠습니다.
1. 보존 법칙의 적분형과 충격 속도 유도
충격파는 물리량이 불연속적으로 변하는 면이므로, 미분형 보존 법칙 $\partial_t q + \partial_x f(q) = 0$을 직접 적용하기 어렵습니다. 대신 적분 형태의 보존 법칙을 이용하여 불연속면을 포함하는 공간 구간 $[x_L(t), x_R(t)]$에서 $q$의 총량 변화를 분석해 보겠습니다. 이 구간의 양 끝점 $x_L(t)$와 $x_R(t)$는 시간에 따라 움직일 수 있으며, 각각 $\dot{x}_L$과 $\dot{x}_R$의 속도로 이동한다고 가정합니다.
구간 내 $q$의 총량은 $\int_{x_L(t)}^{x_R(t)} q(x, t)\,dx$로 표현됩니다. 이 총량의 시간 변화율은 라이프니츠 적분 법칙(Leibniz integration rule)을 적용하여 다음과 같이 계산할 수 있습니다.
\[\frac{d}{dt} \int_{x_L(t)}^{x_R(t)} q(x, t)\,dx = \int_{x_L(t)}^{x_R(t)} \frac{\partial q}{\partial t}\,dx + q(x_R, t)\,\dot{x}_R - q(x_L, t)\,\dot{x}_L\]물리적으로 이 식은 구간 내 $q$의 총량 변화가 두 가지 요인으로 인해 발생함을 나타냅니다: (1) 구간 내부에서 $q$ 자체의 시간 변화($\int q_t\,dx$ 항)와 (2) 움직이는 경계를 통해 들어오거나 나가는 $q$의 양($q(x_R)\dot{x}_R$ 및 $q(x_L)\dot{x}_L$ 항).
이제 원래의 미분형 보존 법칙 $q_t = -f_x$를 첫 번째 항에 대입합니다. 미적분학의 기본 정리에 의해,
\[\int_{x_L(t)}^{x_R(t)} \frac{\partial q}{\partial t}\,dx = -\int_{x_L(t)}^{x_R(t)} \frac{\partial f}{\partial x}\,dx = -\bigl[f(q(x_R, t)) - f(q(x_L, t))\bigr]\]이 식은 구간 내 $q$의 총 변화율이 경계를 통해 들어오고 나가는 순 플럭스(net flux)와 동일하다는 것을 의미합니다. 위 두 결과를 합치면 다음과 같은 관계식을 얻습니다.
\[\frac{d}{dt} \int_{x_L(t)}^{x_R(t)} q(x, t)\,dx = -\bigl[f(q(x_R, t)) - f(q(x_L, t))\bigr] + q(x_R, t)\,\dot{x}_R - q(x_L, t)\,\dot{x}_L\]충격파는 매우 좁은 영역에서 발생하는 불연속입니다. 이 불연속면이 $u_s$의 속도로 전파된다고 합시다. 충격파를 포함하는 제어 부피(control volume)가 충격파와 함께 이동한다고 가정하면, 즉 구간의 양 끝점이 충격파와 동일한 속도로 움직인다면 $\dot{x}_L = \dot{x}_R = u_s$가 됩니다. 이 조건을 위 식에 대입하면:
\[\frac{d}{dt} \int_{x_L(t)}^{x_R(t)} q(x, t)\,dx = -\bigl[f(q_R) - f(q_L)\bigr] + u_s (q_R - q_L)\]여기서 $q_L = q(x_L, t)$와 $q_R = q(x_R, t)$는 각각 충격파 왼쪽과 오른쪽에서의 $q$ 값입니다.
이제 충격파의 두께가 무시할 만큼 작다고 가정하고, 구간의 폭을 0으로 줄이는 극한 $x_R(t) \to x_L(t)$을 생각해 봅시다. $q$가 유한한 값(bounded)을 가진다고 가정하면, 적분 구간의 길이가 0으로 수렴하므로 적분 값과 그 시간 미분 역시 0이 됩니다:
\[\lim_{x_R \to x_L} \frac{d}{dt} \int_{x_L(t)}^{x_R(t)} q(x, t)\,dx = 0\]따라서 다음 관계식이 성립합니다:
\[0 = -\bigl[f(q_R) - f(q_L)\bigr] + u_s (q_R - q_L)\]이 식을 정리하면 충격파 속도 $u_s$를 결정하는 유명한 랭킨-위고니오 조건(Rankine–Hugoniot condition)을 얻을 수 있습니다.
불연속면을 가로지르는 물리량의 변화를 간결하게 표현하기 위해, 점프(jump)를 $[\cdot]$ 기호로 표기하겠습니다. 즉, 임의의 물리량 $\psi$에 대해 $[\psi] = \psi_R - \psi_L$로 정의합니다. (참고: 일부 문헌에서는 $[\psi] = \psi_L - \psi_R$로 정의하기도 하므로 주의가 필요합니다. 여기서는 $R-L$ 규칙을 따릅니다.) 이 표기법을 사용하면 랭킨-위고니오 조건은 다음과 같이 간결하게 표현됩니다:
\[\boxed{\, u_s [q] = [f] \,}\]또는, $[q] \neq 0$인 경우,
\[\boxed{\, u_s = \frac{[f]}{[q]} = \frac{f(q_R) - f(q_L)}{q_R - q_L} \,}\]이 조건은 충격파가 전파될 때, 그 속도 $u_s$는 불연속면을 가로지르는 플럭스의 변화량 $[f]$과 보존량 자체의 변화량 $[q]$의 비율과 같아야 함을 의미합니다. 다시 말해, 충격파는 보존 법칙을 만족시키기 위해 정확히 이 속도로 움직여야 합니다.
2. 랭킨-위고니오 조건의 의미
앞서 유도한 랭킨-위고니오 조건은 충격파와 같은 불연속면의 전파 속도를 결정하는 핵심 관계식입니다.
\[\boxed{\, u_s [q] = [f] \,} \quad \text{또는} \quad \boxed{\, u_s = \frac{f(q_R) - f(q_L)}{q_R - q_L} \,}\]여기서 $[q] = q_R - q_L$와 $[f] = f(q_R) - f(q_L)$는 각각 보존량 $q$와 그 플럭스 $f(q)$의 불연속면 전후 차이를 나타냅니다. 이 조건은 질량, 운동량, 에너지 등 다양한 보존량에 대한 물리 시스템에서 충격파의 속도를 계산하는 데 널리 활용됩니다.
3. 약한 충격파의 속도 ($|q_L-q_R|\ll1$)
플럭스 함수 $f(q)$를 $q_R$ 근방에서 테일러 전개하면 ($[q]=q_R-q_L$ 이므로 $q_L = q_R - [q]$):
\[f(q_L) = f(q_R - [q]) = f(q_R) - f'(q_R)[q] + \tfrac12 f''(q_R)[q]^2 - \mathcal O([q]^3)\]따라서 플럭스의 점프는 다음과 같이 근사할 수 있습니다: \([f] = f(q_R) - f(q_L) = f'(q_R)[q] - \tfrac12 f''(q_R)[q]^2 + \mathcal O([q]^3)\)
이를 랭킨-위고니오 조건 $u_s = [f]/[q]$에 대입하면:
\[u_s = f'(q_R) - \tfrac12 f''(q_R)[q] + \mathcal O([q]^2)\]충격파의 강도 $[q] \to 0$ 극한에서, 충격파 속도는 국소적 특성 속도 $c(q)=df/dq$로 수렴합니다:
\[\lim_{[q]\to0} u_s = f'(q_R) = \frac{df}{dq}\bigg|_{q=q_R} = c(q_R)\]따라서, 불연속의 크기가 매우 작은 약한 충격파(weak shock)는 실질적으로 정보가 전파되는 속도인 특성 속도로 이동하며, 이는 약한 충격파가 점차 선형 파동과 유사하게 동작함을 의미합니다.
4. 물리적 해석 — 가스 역학 예시
압축성 유체를 기술하는 오일러 방정식의 1차원 질량 보존식 $\partial_t \rho + \partial_x (\rho u) = 0$을 살펴봅시다. 이 경우, 보존량 $q$는 밀도 $\rho$에 해당하고, 플럭스 $f(q)$는 질량 플럭스 $\rho u$입니다. 여기서 $u$는 유체의 속도입니다. 랭킨-위고니오 조건을 적용하면 충격파 속도는 다음과 같습니다:
\[u_s = \frac{[f]}{[q]} = \frac{f_R - f_L}{q_R - q_L} = \frac{(\rho u)_R - (\rho u)_L}{\rho_R - \rho_L}\]이 식은 충격파를 가로지르는 질량 플럭스의 변화량과 밀도의 변화량 비율로 충격파 속도를 결정합니다. 이 관계식은 운동량 및 에너지 보존에 대한 랭킨-위고니오 조건과 함께 사용되어, 충격파 전후 상태를 연결하는 완전한 대수적 관계식(shock-adiabatic relations)을 형성합니다.
불연속의 크기가 매우 작아지는 약한 충격파의 경우($|\rho_R - \rho_L| \to 0$, $|u_R - u_L| \to 0$), 충격파 속도 $u_s$는 유체 속도 $u$에 음속 $c$ (여기서 $c$는 $\sqrt{\left(\frac{\partial P}{\partial \rho}\right)_S}$로 정의되는 음파의 속도)를 더하거나 뺀 값으로 수렴합니다: $u_s \to u \pm c$. 이는 약한 충격파가 본질적으로 음파와 유사하게 전파됨을 보여줍니다.
5. 간단한 계산 예제 — 버거스 방정식
비선형 보존 법칙의 가장 단순한 형태 중 하나인 비점성 버거스 방정식(inviscid Burgers equation) $\partial_t q + \partial_x (\tfrac{1}{2} q^2) = 0$을 살펴봅시다. 여기서 보존량은 $q$ (일반적으로 속도로 해석됨)이며, 플럭스는 $f(q) = \tfrac{1}{2} q^2$입니다. 랭킨-위고니오 조건을 적용하면 충격파 속도는 다음과 같이 간단하게 계산됩니다:
\[u_s = \frac{[f]}{[q]} = \frac{\tfrac{1}{2} q_R^2 - \tfrac{1}{2} q_L^2}{q_R - q_L} = \frac{\tfrac{1}{2} (q_R - q_L)(q_R + q_L)}{q_R - q_L} = \frac{q_L + q_R}{2}\]흥미롭게도, 버거스 방정식에서 충격파 속도는 충격파 양쪽 상태값의 단순 평균과 같습니다. 예를 들어, 충격파 왼쪽 상태가 $q_L=1$이고 오른쪽 상태가 $q_R=0$이라면, 충격파 속도는 $u_s = (1+0)/2 = 0.5$입니다. 또 다른 예로, $q_L=2$, $q_R=1$인 경우 충격파 속도는 $u_s = (2+1)/2 = 1.5$가 됩니다.
6. 결론
- 1차원 보존 법칙 $\partial_t q + \partial_x f(q) = 0$의 불연속 해인 충격파의 전파 속도 $u_s$는 랭킨-위고니오 조건 $u_s [q] = [f]$에 의해 결정됩니다.
- 충격파 속도는 보존량 $q$의 변화량 $[q]$와 플럭스 $f(q)$의 변화량 $[f]$ 사이의 비율, 즉 $u_s = [f]/[q]$로 주어집니다.
- 불연속의 크기($[q]$)가 0에 가까워지는 극한에서, 충격파 속도는 국소적 특성 속도 $c(q)=df/dq$로 수렴합니다. 이는 약한 충격파가 선형 파동처럼 전파됨을 의미합니다.
- 이 원리는 버거스 방정식이나 오일러 방정식과 같은 다양한 물리 시스템에 적용되어 충격파의 동역학을 이해하는 데 활용됩니다.