Riemann Problem - WHAT?
What is the Riemann Problem?
Hyperbolic PDEs often exhibit discontinuous solutions, such as shock waves and contact discontinuities. The challenge lies in accurately capturing these abrupt changes in the solution. One key problem in this context is the Riemann problem, which is a specific initial value problem for hyperbolic PDEs. It involves a piecewise constant initial condition, leading to the formation of discontinuities. The core idea is to solve for the evolution of these discontinuities over time.
Mathematical Formulation of the Riemann Problem
Let us consider a simple conservation law given by the MHD equations for a 1D shock tube problem:
\[\frac{\partial \mathbf{u}}{\partial t} + \frac{\partial \mathbf{f}(\mathbf{u})}{\partial x} = 0\]where \(\mathbf{u}\) is the vector of conserved quantities (density, momentum, energy, magnetic field components), and \(\mathbf{f}(\mathbf{u})\) is the flux vector.
Conserved Quantities and Fluxes
In MHD, the conserved quantities and their corresponding fluxes are given by:
\[\mathbf{u} = \begin{pmatrix} \rho \\ \rho u \\ \rho v \\ \rho w \\ E \\ B_y \\ B_z \end{pmatrix}, \quad \mathbf{f}(\mathbf{u}) = \begin{pmatrix} \rho u \\ \rho u^2 + p^* - B_x^2 \\ \rho u v - B_x B_y \\ \rho u w - B_x B_z \\ (E + p^*)u - B_x (\mathbf{B} \cdot \mathbf{v}) \\ u B_y - v B_x \\ u B_z - w B_x \end{pmatrix}\]where:
- \(\rho\) is the density.
- \(\mathbf{v} = (u, v, w)\) is the velocity vector.
- \(\mathbf{B} = (B_x, B_y, B_z)\) is the magnetic field vector.
- \(E = \frac{\rho (\mathbf{v} \cdot \mathbf{v})}{2} + \frac{p}{\gamma - 1} + \frac{\mathbf{B} \cdot \mathbf{B}}{2}\) is the total energy density.
- \(p^* = p + \frac{\mathbf{B} \cdot \mathbf{B}}{2}\) is the total pressure including magnetic pressure.
Piecewise Constant Initial Conditions
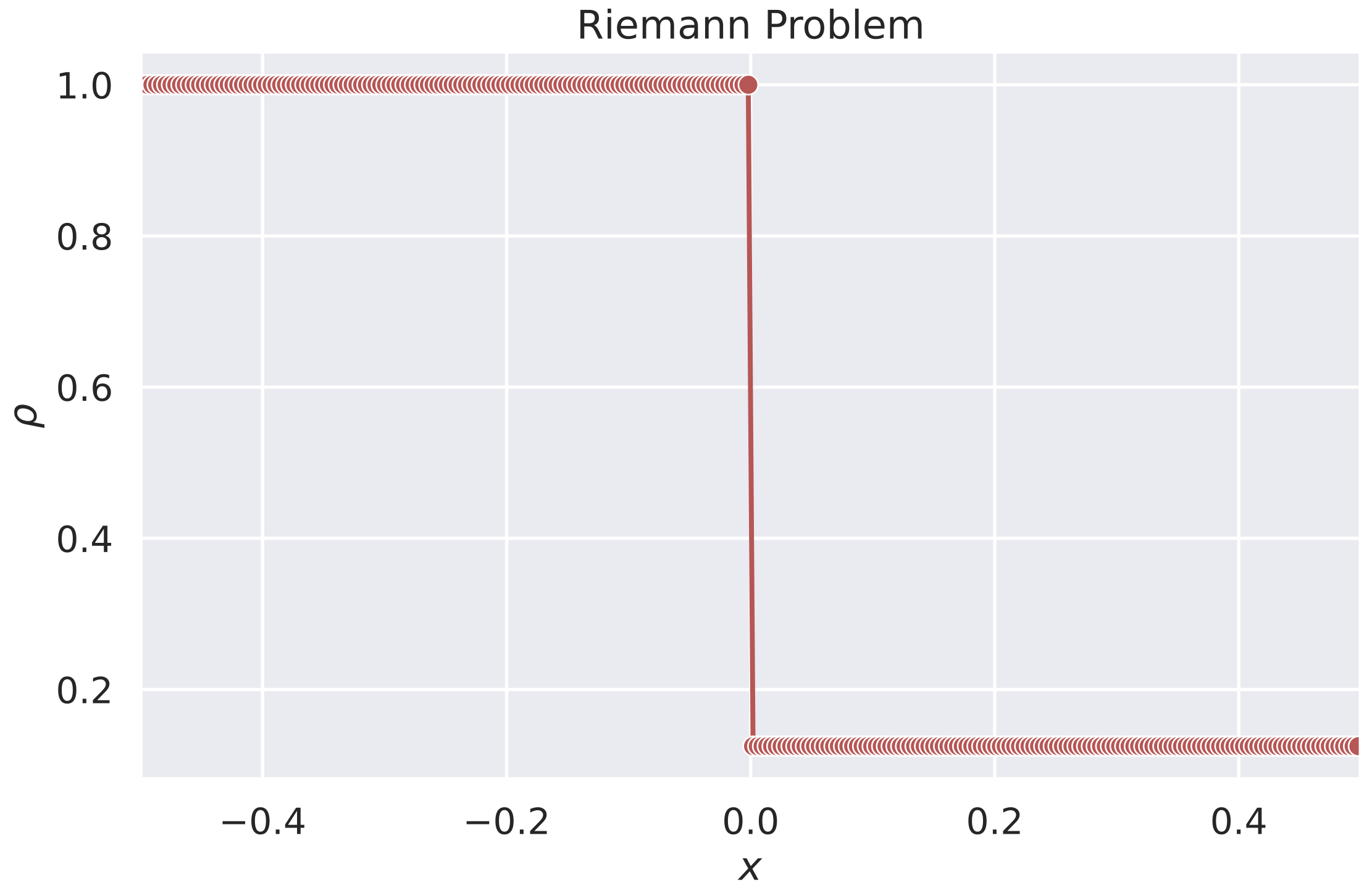
The Riemann problem initially provides the piecewise constant, representing a discontinuity at \(x = 0\):
\[\mathbf{u}(x, 0) = \begin{cases} \mathbf{u}_L & \text{if } x < 0 \\ \mathbf{u}_R & \text{if } x \geq 0 \end{cases}\]where \(\mathbf{u}_L\) and \(\mathbf{u}_R\) are the states to the left and right of the discontinuity, respectively.
Step-by-Step Solution Process
1. Determine Eigenvalues and Eigenvectors
The Jacobian matrix of the flux vector \(\mathbf{A} = \frac{\partial \mathbf{f}}{\partial \mathbf{u}}\) has the eigenvalues:
\[\lambda_1, \lambda_2, \lambda_3, \lambda_4, \lambda_5, \lambda_6, \lambda_7\]These eigenvalues correspond to the speeds of the various waves in MHD, including the fast and slow magnetosonic waves, the Alfvén wave, and the contact discontinuity. Specifically:
- Fast magnetosonic waves: \(\lambda_1, \lambda_7\)
- Alfvén waves: \(\lambda_2, \lambda_6\)
- Slow magnetosonic waves: \(\lambda_3, \lambda_5\)
- Contact discontinuity: \(\lambda_4\)
The eigenvalues are given by:
\[\begin{aligned} &\lambda_1 = u - c_f \\ &\lambda_2 = u - v_A \\ &\lambda_3 = u - c_s \\ &\lambda_4 = u \\ &\lambda_5 = u + c_s \\ &\lambda_6 = u + v_A \\ &\lambda_7 = u + c_f \end{aligned}\]where:
- \(c_f\) is the fast magnetosonic speed.
- \(v_A\) is the Alfvén speed.
- \(c_s\) is the slow magnetosonic speed.
The corresponding eigenvectors \(\mathbf{r}_i\) are:
\[\mathbf{r}_1 = \begin{pmatrix} 1 \\ u - c_f \\ v \\ w \\ H - uc_f \\ B_y \\ B_z \end{pmatrix}, \quad \mathbf{r}_2 = \begin{pmatrix} 0 \\ 0 \\ B_z \\ -B_y \\ v_A B_x \\ u B_y - v_A B_y \\ u B_z - v_A B_z \end{pmatrix}, \quad \mathbf{r}_3 = \begin{pmatrix} 1 \\ u - c_s \\ v \\ w \\ H - uc_s \\ B_y \\ B_z \end{pmatrix}\]2. Solve for Shock Waves
For a shock wave, the Rankine-Hugoniot conditions must be satisfied:
\[s [\mathbf{u}] = [\mathbf{f}(\mathbf{u})]\]For each conserved quantity, we can write the conditions as:
\[s (\rho_R - \rho_L) = \rho_R u_R - \rho_L u_L\] \[s (\rho_R u_R - \rho_L u_L) = \rho_R u_R^2 + p^*_R - B_{xR}^2 - (\rho_L u_L^2 + p^*_L - B_{xL}^2)\] \[s (\rho_R v_R - \rho_L v_L) = \rho_R u_R v_R - \rho_L u_L v_L - B_{xR} B_{yR} + B_{xL} B_{yL}\] \[s (\rho_R w_R - \rho_L w_L) = \rho_R u_R w_R - \rho_L u_L w_L - B_{xR} B_{zR} + B_{xL} B_{zL}\] \[s (E_R - E_L) = u_R \left(E_R + p^*_R - B_{xR}^2\right) - u_L \left(E_L + p^*_L - B_{xL}^2\right)\]The magnetic field components normal to the shock must also satisfy:
\[s (B_{yR} - B_{yL}) = u_R B_{yR} - u_L B_{yL}\] \[s (B_{zR} - B_{zL}) = u_R B_{zR} - u_L B_{zL}\]3. Solve for Rarefaction Waves
For a rarefaction wave, the solution is continuous and follows the integral curves of the characteristic equations. The rarefaction wave solution can be expressed as:
\[u(x,t) = \begin{cases} u_L & \text{if } x < \lambda_1 t \\ \phi(x/t) & \text{if } \lambda_1 t \leq x \leq \lambda_7 t \\ u_R & \text{if } x > \lambda_7 t \end{cases}\]For the MHD equations, the rarefaction wave involves solving the characteristic equations:
\[\frac{d \mathbf{u}}{d \xi} = \frac{\partial \mathbf{f}(\mathbf{u})}{\partial \mathbf{u}} \mathbf{r}_i \quad \text{where} \quad \xi = \frac{x}{t}\]4. Determine Intermediate States
To find the intermediate states \(\mathbf{u}^*\) between the left and right states, we need to solve the nonlinear system of equations formed by the Rankine-Hugoniot conditions for shocks and the integral curves for rarefactions.
For example, consider the following steps:
- Assume an initial guess for the pressure \(p^*\) in the intermediate state.
- Use this guess to compute the density \(\rho^*\), velocity \(u^*\), and magnetic field components \(\mathbf{B}^*\) using the equations of state and conservation laws.
- Iterate on \(p^*\) until the Rankine-Hugoniot conditions and the rarefaction integral curves are satisfied for both left and right states.
5. Assemble the Solution
The final solution \(\mathbf{u}(x, t)\) consists of multiple states separated by seven waves (shock or rarefaction):
- Left state \(\mathbf{u}_L\)
- Left intermediate states \(\mathbf{u}^*_L\)
- Right intermediate states \(\mathbf{u}^*_R\)
- Right state \(\mathbf{u}_R\)
These states are connected by the shock, rarefaction, and Alfvén waves propagating at their respective speeds.
Detailed Example: MHD Shock Tube Problem
Let’s go through a detailed example of solving the Riemann problem for an MHD shock tube problem with given initial conditions.
Initial Conditions
\[\mathbf{u}_L = \begin{pmatrix} \rho_L \\ \rho_L u_L \\ \rho_L v_L \\ \rho_L w_L \\ E_L \\ B_{xL} \\ B_{yL} \\ B_{zL} \end{pmatrix} = \begin{pmatrix} 1.0 \\ 0 \\ 0 \\ 0 \\ 2.5 \\ 1.0 \\ 0 \\ 0 \end{pmatrix}, \quad \mathbf{u}_R = \begin{pmatrix} \rho_R \\ \rho_R u_R \\ \rho_R v_R \\ \rho_R w_R \\ E_R \\ B_{xR} \\ B_{yR} \\ B_{zR} \end{pmatrix} = \begin{pmatrix} 0.125 \\ 0 \\ 0 \\ 0 \\ 0.25 \\ 1.0 \\ 0 \\ 0 \end{pmatrix}\]Steps
Compute the sound speeds \(c_s\):
\[c_s = \sqrt{\frac{\gamma p}{\rho}}\]Compute the Alfvén speeds \(v_A\):
\[v_A = \frac{B_x}{\sqrt{\rho}}\]Compute the fast and slow magnetosonic speeds \(c_f\) and \(c_s\):
\[c_{f,s} = \sqrt{\frac{\gamma p + |\mathbf{B}|^2 \pm \sqrt{(\gamma p + |\mathbf{B}|^2)^2 - 4 \gamma p B_x^2}}{2 \rho}}\]Solve the Rankine-Hugoniot conditions for the shock, Alfvén, and rarefaction waves to find the intermediate states:
- Use the computed wave speeds to determine the intermediate states between the left and right states by solving the Rankine-Hugoniot conditions: \(s [\mathbf{u}] = [\mathbf{f}(\mathbf{u})]\) where \(s\) is the shock speed, \(\mathbf{u}\) is the vector of conserved quantities, and \(\mathbf{f}(\mathbf{u})\) is the flux vector.
These conditions ensure that mass, momentum, and energy are conserved across the discontinuities (shocks and rarefactions). For each conserved quantity, the Rankine-Hugoniot condition can be written as:
\[s (\rho_R - \rho_L) = \rho_R u_R - \rho_L u_L\] \[s (\rho_R u_R - \rho_L u_L) = \rho_R u_R^2 + p_R - (\rho_L u_L^2 + p_L)\] \[s (\rho_R v_R - \rho_L v_L) = \rho_R u_R v_R - \rho_L u_L v_L\] \[s (\rho_R w_R - \rho_L w_L) = \rho_R u_R w_R - \rho_L u_L w_L\] \[s (E_R - E_L) = u_R (E_R + p_R) - u_L (E_L + p_L)\]
Iterate to find the correct intermediate pressure \(p^*\) and velocities \(u^*_L\), \(u^*_R\), and intermediate magnetic field components:
- Start with an initial guess for the intermediate pressure \(p^*\).
Use this guess to calculate the corresponding densities, velocities, and magnetic fields in the intermediate states. The intermediate states can be solved using the shock and rarefaction equations:
\[\rho^* = \frac{\rho_L + \rho_R}{2}\] \[u^* = \frac{u_L + u_R}{2}\] \[B^*_x = \frac{B_{xL} + B_{xR}}{2}\]- Iterate this process until the Rankine-Hugoniot conditions and continuity of the characteristics are satisfied.
Assemble the solution \(\mathbf{u}(x,t)\) with the identified waves and intermediate states:
The final solution \(\mathbf{u}(x,t)\) is constructed by piecing together the left and right states, as well as the intermediate states, separated by the various waves:
\[\mathbf{u}(x,t) = \begin{cases} \mathbf{u}_L & \text{if } x < s_L t \\ \mathbf{u}^* & \text{if } s_L t \leq x \leq s_R t \\ \mathbf{u}_R & \text{if } x > s_R t \end{cases}\]This involves determining the positions and strengths of shocks, rarefactions, and contact discontinuities.
Summary and Further Steps
The Riemann problem for hyperbolic PDEs such as the MHD equations involves understanding and solving for the interactions of shock waves, rarefaction waves, Alfvén waves, and contact discontinuities. This detailed mathematical process provides the foundation for more advanced numerical methods and applications.