Convective Magnetic Flux Emergence Simulations from the Deep Solar Interior to the Photosphere: Comprehensive Study of Flux Tube Twist (Toriumi, S., 2024)
Presented by: Donghui Son
Solar Physics Journal Club @ KHU
Introduction
Purpose of this study
Investigate how varying initial twist in deeply rooted magnetic flux tubes influences their emergence, helicity injection, and sunspot formation.
Background
Sunspots and Active Regions (ARs) arise when toroidal magnetic flux tubes formed in the convection zone rise to the photosphere.
As a magnetic flux emerges, it supplies magnetic helicity to the corona, thereby accumulating free magnetic energy and ultimately triggering explosive events such as flares.
The twist of emerging magnetic flux is highlighted as a key factor governing generation, transport, and release of a magnetic field.
This study focuses on the role of magnetic twist in the process.
Importance of magnetic twist in emerging flux
Without sufficient twist, a flux tube can be shredded by surrounding convective flows and fail to reach the photosphere.
A certain level of twist has been considered essential for magnetic integrity.
Key findings from previous MHD simulations
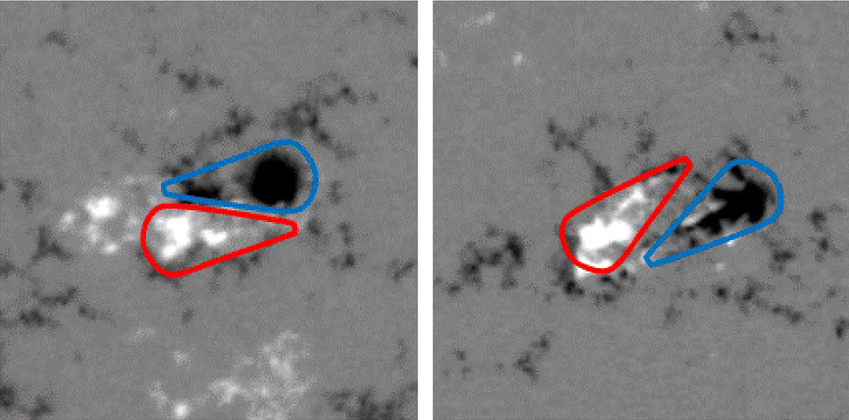
- Twisted flux tubes emerge with distinct positive/negative polarity pattern (i.e., yin-yang pattern called “magnetic tongues”)
- tilt angle of the two spots
- sunspot rotation
- injecting free energy and magnetic helicity into the corona
- Higher initial twist:
- faster rise through the CZ
- more pronounced sunspot rotation
- stronger free energy injection
Examples of yin-yang pattern
Flare-active ARs and complex magnetic fields
- Observations show highly flare-productive ARs often have:
- Complex magnetic configurations
- $\delta$-type sunspots (opposite polarities in one penumbra)
- Kink Instability Hypothesis:
- Occurs when twist exceeds critical threshold
- Causes flux tube to writhe and deform
- Can produce complex $\delta$-spot structures
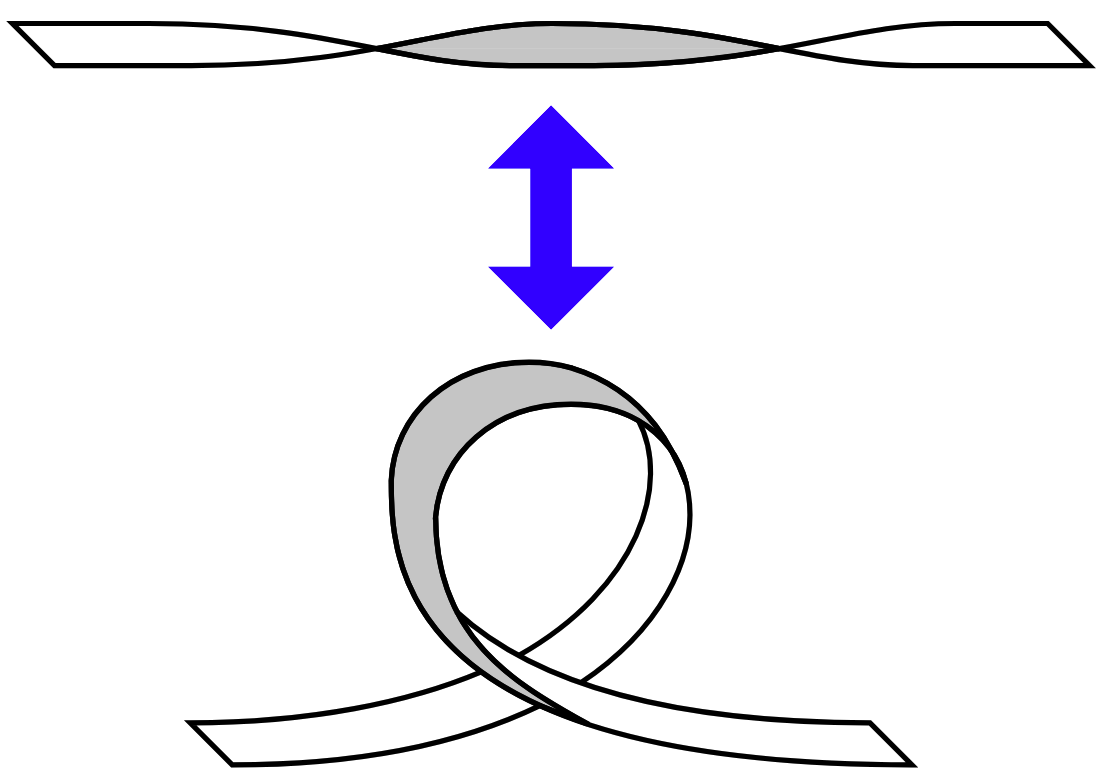
Previous studies
Key previous findings
- Tanaka (1991): $\delta$-spots from twisted ropes
- Linton et al. (1996, 1999): Theoretical kink criterion
- Fan (1998, 1999): Kink produces writhing tubes
- Takasao et al. (2015): Kink drives polarities rotation
- Toriumi & Takasao (2018): Kink supplies the greatest free energy.
- Knizhnik et al. (2018): Tested extreme twist values (up to $4q_{cr}$)
Limitation in previous studies
Most prior models did not account for realistic convective turbulence
Key question and current approach
Is kink instability genuinely feasible under realistic solar conditions?
What sets this study apart
- Incorporates realistic solar thermal convection
- Tests twist values from zero to twice kink threshold
Numerical model: R2D2
Radiation and Reduced Speed of Sound Technique for Deep Dynamics
MHD Equations (Anelastic Approximation with RSST):
\[\frac{\partial \rho_{1}}{\partial t} = -\frac{1}{\xi^{2}} \,\nabla \cdot \bigl(\rho\,\mathbf{V}\bigr)\] \[\frac{\partial (\rho \mathbf{V})}{\partial t} = -\,\nabla\cdot \bigl(\rho\,\mathbf{V}\,\mathbf{V}\bigr) \;-\;\nabla p_{1} \;+\;\rho_{1}\,\mathbf{g} \;+\;\frac{1}{4\pi} \Bigl((\nabla\times\mathbf{B})\times \mathbf{B}\Bigr)\] \[\frac{\partial \mathbf{B}}{\partial t} = \nabla \times \bigl(\mathbf{V}\times \mathbf{B}\bigr)\] \[\rho\,T\;\frac{\partial s_{1}}{\partial t} = \rho\,T \bigl(\mathbf{V}\cdot \nabla\bigr)s \;+\;Q\] \[p_{1} = p_{1}(\rho, s)\]Variable Decomposition:
\[\rho = \rho_{0} + \rho_{1}\] \[p = p_{0} + p_{1}\] \[s = s_{0} + s_{1}\]Numerical model: R2D2 (Details)
- Self-consistently simulates convective motions and radiative transfer throughout the solar convection zone.
- Adopts the Model S solar structure (for density, pressure, temperature stratification) as an initial static background, along with a realistic equation of state including partial ionization.
- Radiative transfer is solved using a gray approximation and Rosseland mean opacity in both upward and downward directions, enabling accurate modeling of photospheric cooling and internal heating, thus driving convection.
Numerical model: R2D2 (Domain)
Domain specifications
- 3D Cartesian grid:
- ($L_x , L_y , L_z ) = (98.3 \text{ Mm}, 98.3 \text{ Mm}, 201.7 \text{ Mm}$)
- ($N_x , N_y , N_z ) = (1024, 1024, 384$): non-uniform grids for $\Delta z$
- Boundary conditions:
- Periodic boundaries horizontally
- Potential field (open) boundary at top ($z=700 \text{ km}$ above the $\tau=1$ surface)
- Stress-free at bottom boundary ($z=201 \text{ Mm}$ below the $\tau=1$ surface):
- Upward convective (thermal) flux is supplied, mimicking the Sun’s radiative energy input from below.
- Open for downward flow
Reduced speed-of-sound technique (RSST)
- In the CZ, sound speed ($c_s$) is extremely high, making a direct simulation with full compressibility prohibitively time-consuming.
- Artificially reduces $c_s \rightarrow$ Relaxes the CFL condition $\rightarrow$ Allows larger $\Delta t$.
The RSST factor $\xi$
\[\xi (z)=\max \left(1,{\xi }_{0}{\left[\displaystyle \frac{{\rho }_{0}(z)}{{\rho }_{{\rm{b}}}}\right]}^{1/3},\displaystyle \frac{{c}_{{\rm{s}}}(z)}{{c}_{{\rm{b}}}}\right), \quad {c}_{{\rm{s}}}(z)=\sqrt{{\left(\partial p/\partial \rho \right)}_{{\rm{s}}}}\]
- $\xi_0=160$ is a constant factor
- $\rho_b=0.2$ g cm$^{-3}$ is the density around the bottom of the CZ
- $c_b=2.2 \times 10^7$ cm s$^{-1}$ is the sound speed around the bottom of the CZ
- $c_s(z)$ is the local adiabatic sound speed.
Simulation methodology
- Initial hydrodynamic phase:
- Starts with magnetically free convection simulation
- Imposes heat flux at lower boundary
- Top boundary radiates energy away
- Development of natural convection:
- System evolves to statistically steady state
- Forms large-scale downflow plumes and upflow cells
- Creates realistic solar convective environment
- Magnetic flux introduction:
- Horizontal flux tube inserted into established convective flow
- Various twist parameters tested (from zero to twice kink threshold)
Initial magnetic flux tube
Horizontal magnetic flux tube introduced into the domain at about $20-30 \text{ Mm}$ below the surface:
\[{B}_{x}(r) = {B}_{\mathrm{tb}}\exp \left(-\displaystyle \frac{{r}^{2}}{{R}_{\mathrm{tb}}^{2}}\right), \quad {B}_{\phi }(r) ={{qrB}}_{x}(r)\](Note: Paper uses $B_{tb}(r)$ instead of $B_x(r)$ in the $B_{\phi}(r)$ definition, corrected here based on typical flux tube models)
- $B_{\mathrm{tb}}$: axial field strength
- $r$: radial distance from the center of the tube
- $\phi$: azimuthal angle
- $R_{\mathrm{tb}}$: tube radius ($= 8$ Mm)
- $q$: twist strength
$\rightarrow$ Gaussian flux tube
Initial magnetic flux tube (Image)
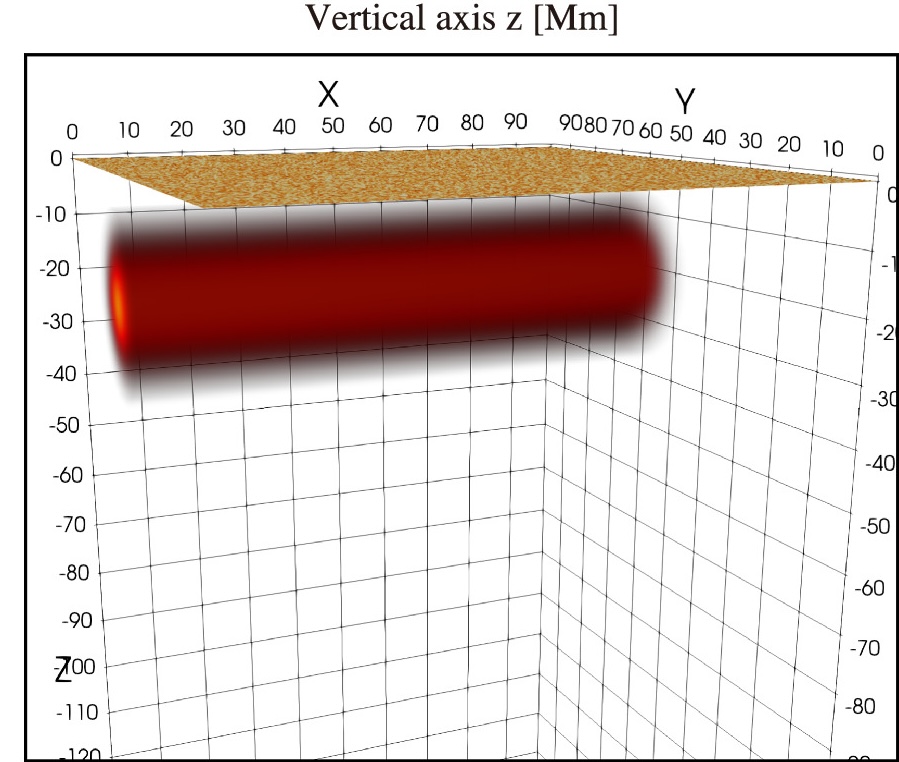
Initial magnetic flux tube (Buoyancy)
No initial buoyancy
Pressure excess inside the tube relative to the exterior:
\[\delta {p}_{\mathrm{exc}}(r)=\frac{{B}_{x}^{2}(r)}{8\pi}\left[{q}^{2}\left(\frac{{R}_{\mathrm{tb}}^{2}}{2}\right)-1\right]\]This is made negative ($\delta p_{exc} < 0$) by choosing appropriate $q$ and $R_{tb}$. The tube is placed in pressure balance ($\delta p = \delta p_{exc} + \delta p_{gas} = 0$) with its surroundings by adjusting internal entropy ($\delta s$) so that the tube is initially neither more nor less dense than the exterior fluid.
$\rightarrow$ Advected by external flows, not intrinsically buoyant.
Simulation cases
- Nine total simulation cases
- $q/q_{cr} = \left[-2, -1, -1/2, -1/4, 0, +1/4, +1/2, +1, +2\right]$ with $q_{cr} = 1/R_{tb}$
- Positive/negative values represent right-/left-handed twists.
- $|q/q_{cr}| \geq 1$ indicates potentially kink-unstable.
- Adjust the axial field strength $\left(B_{\mathrm{tb}}\right)$ to maintain the same total $E_{mag}$
- All cases have the same initial $E_{mag} = 5.85 \times 10^{34}$ erg
| Case | $B_\text{tb}$ (kG) | $R_\text{tb}$ (Mm) | $q/q_\text{cr}$ | $q$ (Mm$^{-1}$) | $\Phi_x$ (Mx) |
|---|---|---|---|---|---|
| 1 | 7.1 | 8.0 | $-2$ | $-0.25$ | $1.40 \times 10^{22}$ |
| 2 | 10.0 | 8.0 | $-1$ | $-0.125$ | $1.97 \times 10^{22}$ |
| 3 | 11.5 | 8.0 | $-1/2$ | $-0.0625$ | $2.28 \times 10^{22}$ |
| 4 | 12.1 | 8.0 | $-1/4$ | $-0.03125$ | $2.38 \times 10^{22}$ |
| 5 | 12.2 | 8.0 | 0 | 0 | $2.42 \times 10^{22}$ |
| 6 | 12.1 | 8.0 | 1/4 | 0.03125 | $2.38 \times 10^{22}$ |
| 7 | 11.5 | 8.0 | 1/2 | 0.0625 | $2.28 \times 10^{22}$ |
| 8 | 10.0 | 8.0 | 1 | 0.125 | $1.97 \times 10^{22}$ |
| 9 | 7.1 | 8.0 | 2 | 0.25 | $1.40 \times 10^{22}$ |
Analysis methodology (Parameters)
- Measurement height: $z = 200 \text{ km}$ (due to strong downflow at $\tau=1$)
- Temporal averaging: 6-hr moving average applied to all time series data
- Filters out short-term convective fluctuations (10 min to few hrs)
- Preserves emergence dynamics (typical duration: 30-40 hr)
- Total unsigned magnetic flux: $\Phi = \int_{S} |B_z| \, dS$
- Sunspot area $A_{\text{spot}}$:
- Regions where emergent intensity $< 90\%$ of quiet-Sun average
- Twist parameters (calculated for pixels where $|B_z| \geq 100$ G):
- $\alpha_{av}^{0} = \left\langle J_z/B_z \right\rangle$
- $\alpha_{av}^{1} = \frac{\left\langle J_z \text{sgn}(B_z)\right\rangle} {\left\langle|B_z| \right\rangle}$
- $\alpha_{av}^{2} = \frac{\left\langle B_z J_z \right\rangle}{\left\langle B_z^2 \right\rangle}$
Analysis methodology (Fluxes)
Magnetic helicity flux:
\[{F}_{z}=2{\int }_{S}\left[\left({{\boldsymbol{A}}}_{{\rm{p}}}\cdot {{\boldsymbol{B}}}_{{\rm{h}}}\right){V}_{z}-\left({{\boldsymbol{A}}}_{{\rm{p}}}\cdot {{\boldsymbol{V}}}_{{\rm{h}}}\right){B}_{z}\right]{dS}\]($\boldsymbol{A}_p$ is vector potential, $\boldsymbol{B}_h, \boldsymbol{V}_h$ are horizontal components)
Total injected helicity:
\[{\rm{\Delta }}{H}_{{\rm{R}}}={\int }_{0}^{t}{F}_{z}\,{dt}^{\prime}\](related to flare occurrence)
Poynting flux (vertical component):
\[{S}_{z}=\displaystyle \frac{1}{4\pi }{\int }_{S}\left[{B}_{{\rm{h}}}^{2}{V}_{z}-({{\boldsymbol{B}}}_{{\rm{h}}}\cdot {{\boldsymbol{V}}}_{{\rm{h}}}){B}_{z}\right]{dS}\]Total injected magnetic energy:
\[{E}_{\mathrm{mag}}={\int }_{0}^{t}{S}_{z}\,{dt}^{\prime}\](energy injection into the atmosphere)
Results
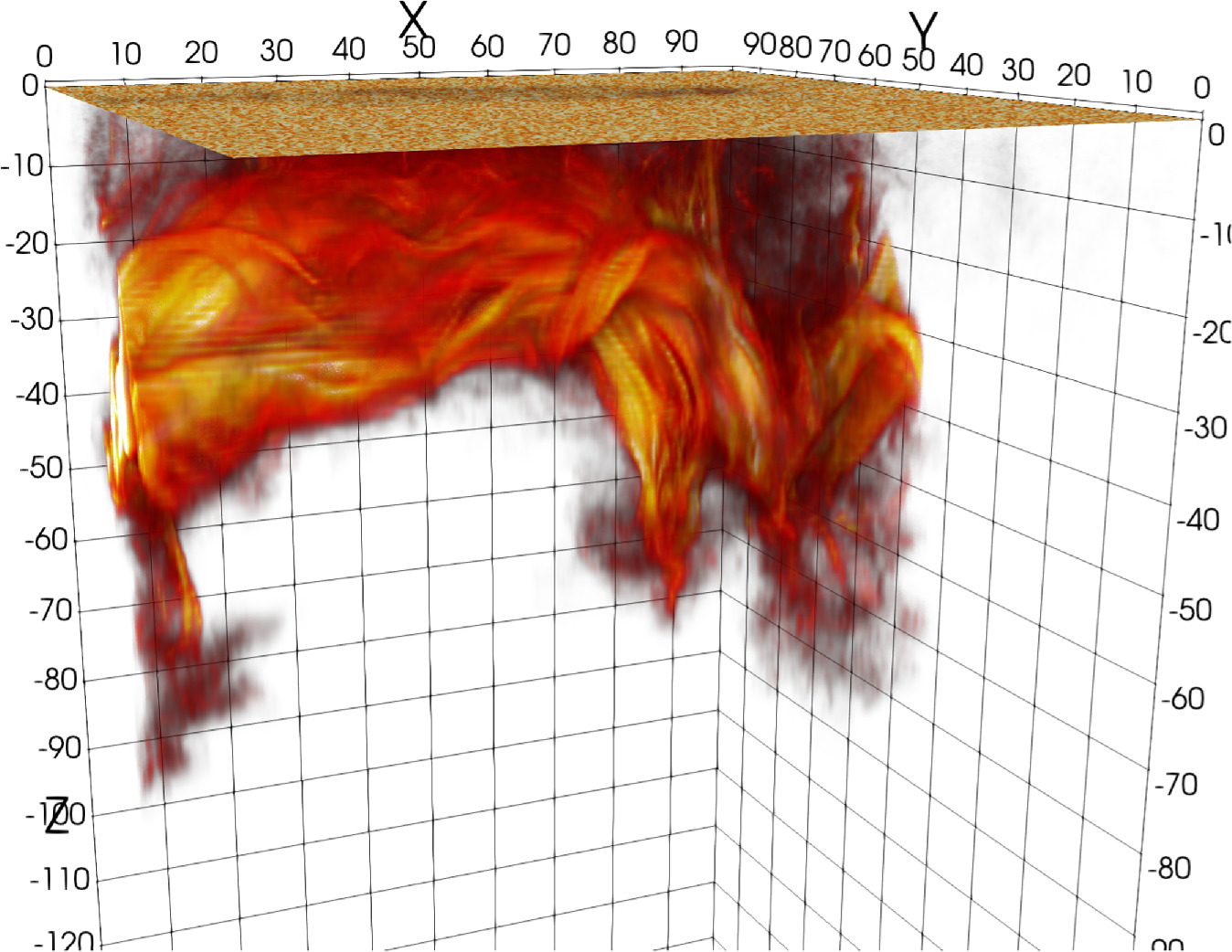
Overall evolution (Visual)
Overall evolution (Temporal Overview)
- Early stage: small fragments of the rising flux tube appear at the surface.
- $t\sim 20$ hr: the main portion emerges via large upflows.
- Emergence forms a yin-yang pattern of positive/negative polarities.
- With periodic boundaries, opposite polarities eventually collide ($t\sim 30$ hr), forming $\delta$-spots ($t\sim 50$ hr).
Key observation: Initial tilt in the untwisted case
A yin-yang pattern or tilt alone does not prove the initial tube was twisted $\rightarrow$ strong turbulence can induce similar appearances even if $q=0$.
Overall evolution (Effect of twist $q/q_{cr}$)
- Even an untwisted tube ($q=0$) can rise via convection.
- Weakly twisted fields ($|q/q_{cr}| = 1/4, 1/2$) diffuse less quickly at the surface than the untwisted case.
- Twist helps maintain flux tube integrity against turbulent shredding.
- Extremely large twist ($|q/q_{cr}| = 2$) also shows a diffuse distribution.
- Initially weaker axial field $B_{tb}$ and smaller total flux $\Phi_x$.
- Relatively more susceptible to influence by surrounding turbulence.
- The sign of helicity injection ($F_z$) depends on the initial twist sign ($q$).
Results (3D Visualization)
Results: (Unsigned) Magnetic flux and sunspot area (Time Series)
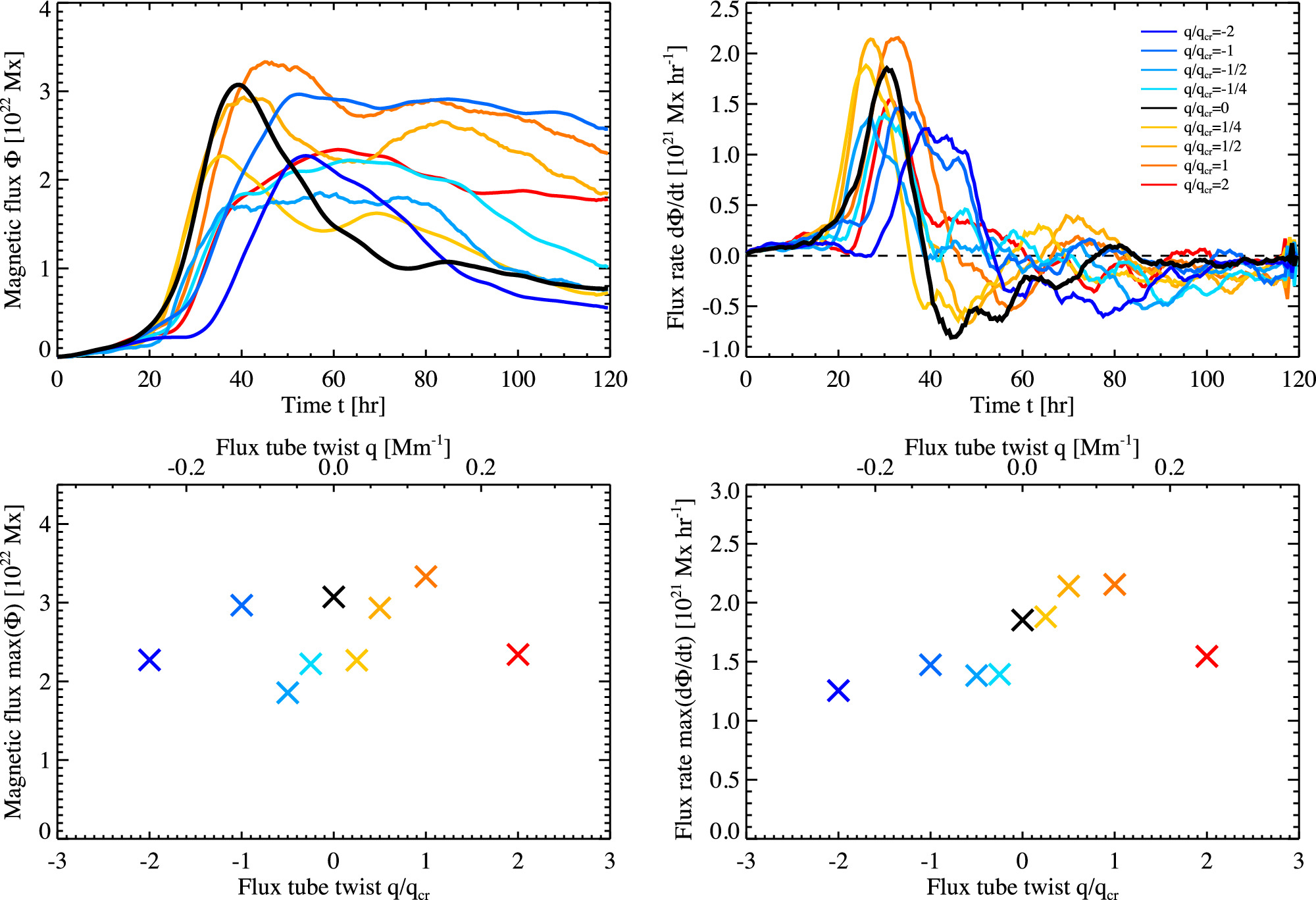
Results: (Unsigned) Magnetic flux and sunspot area (Effect of twist)
- Extremely high twist ($|q/q_{cr}| = 2$) yields a significantly lower peak magnetic flux ($\Phi_{max}$).
- Initial $B_{tb}=7.1$ kG is comparable to the equipartition field strength ($B_{eq} \approx 6.5$ kG at $z_{tb}=-22$ Mm).
- Suggests the tube might be more easily disrupted or collapsed by external turbulence.
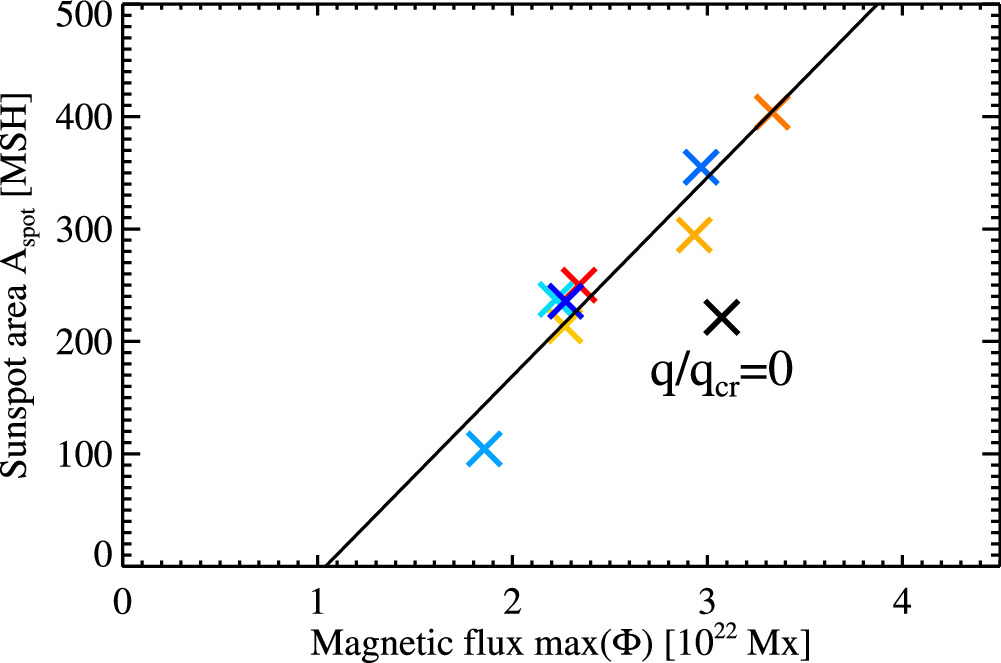
Results: (Unsigned) Magnetic flux and sunspot area (Spot Area vs Flux)
The tendency is that emerging ARs with weaker twist ($|q/q_{cr}| \leq 1/2$) are more scattered and thus have a smaller sunspot area ($A_{spot}$) relative to their maximum emerged flux ($\Phi_{max}$).
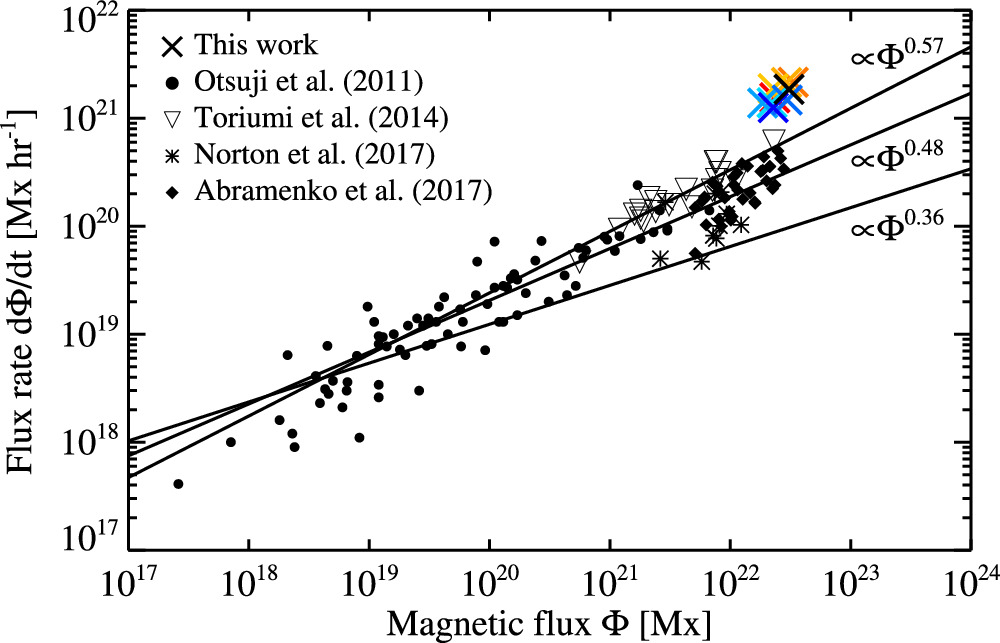
Results: (Unsigned) Magnetic flux and sunspot area (Growth Rate Comparison)
- Simulated flux growth rates ($d\Phi/dt$) are generally higher than observed values from major ARs like NOAA AR 12673.
- Possible reasons: Idealized initial conditions, differences in simulation vs. real Sun dynamics.
Results: Magnetic twist $\alpha_{av}$ (Definition)
Examine how much of the twist in the initial flux tube ($q$) is reflected in the photospheric twist parameter $\alpha_{av}$ after emergence.
Three definitions used (calculated for pixels where $|B_z| \geq 100$ G):
\[\alpha_{av}^{0} = \left\langle J_z/B_z \right\rangle\] \[\alpha_{av}^{1} = \frac{\left\langle J_z \text{sgn}(B_z)\right\rangle}{\left\langle|B_z| \right\rangle}\] \[\alpha_{av}^{2} = \frac{\left\langle B_z J_z \right\rangle}{\left\langle B_z^2 \right\rangle}\]($\alpha_{av}^{2}$ gives more weight to strong-field regions).
Results: Magnetic twist $\alpha_{av}$ (Plot)

Results: Magnetic twist $\alpha_{av}$ (Analysis)
- $max(|\alpha_{av}|)$ generally increases with initial $|q|$, but tends to saturate for higher $|q|$.
- $max(|\alpha_{av}|)$ tends to decrease from $\alpha_{av}^{0}$ to $\alpha_{av}^{2}$, suggesting weaker field regions retain relatively more twist.
- Smaller initial $|q|$ seems to conserve the original twist better during emergence.
- Saturation at higher $|q|$ could be due to:
- Less successful emergence (flux disperses).
- Turbulence stripping away twist.
- Twist mitigation by the upper boundary condition.
Results: Magnetic helicity (Time Series)
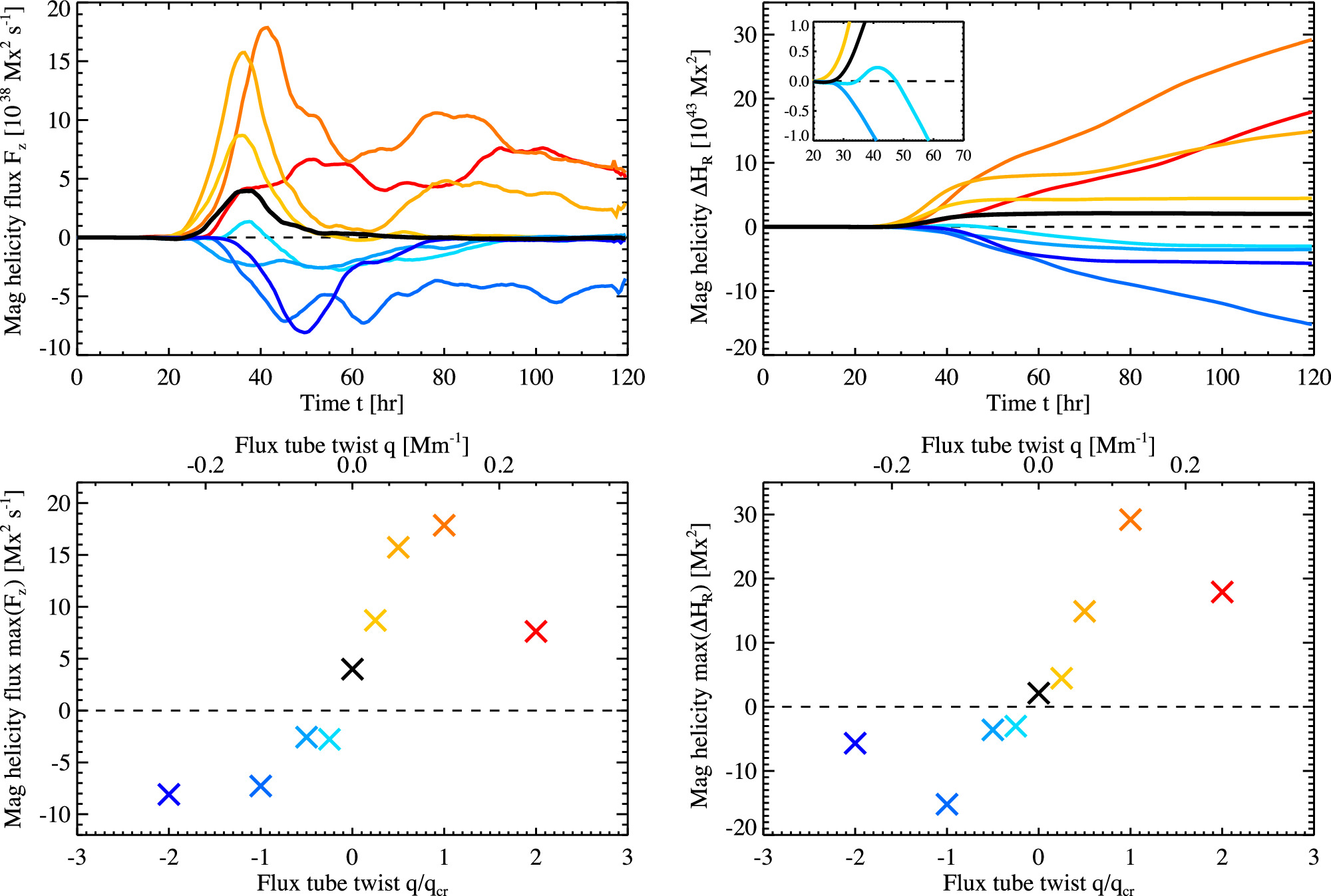
Results: Magnetic helicity (Analysis)
- Peak helicity flux ($F_z$) and total injected helicity ($\Delta H_R$) generally scale with initial twist $q$.
- Even the untwisted case ($q=0$) injects finite positive helicity, likely acquired from convective buffeting.
- For $q/q_{cr} = -1/4$, $F_z$ initially shows positive injection (from convection) before the tube’s negative helicity dominates.
Results: Normalized magnetic helicity
- Normalized helicity $\Delta H_R/\Phi_{max}^2$ is used for comparison with observations.
- Observations suggest typical AR values are $\sim 0.01$, with super-flaring ARs reaching $\leq 0.04$.
- Simulations show that for $|q/q_{cr}| = 1/2$, the normalized helicity already exceeds typical observed levels ($> 0.1$).
Key Implication: Initial twist above the kink threshold ($|q/q_{cr}| \geq 1$) seems to produce unrealistically large helicity injection compared to observations.
Results: Magnetic energy (Time Series)
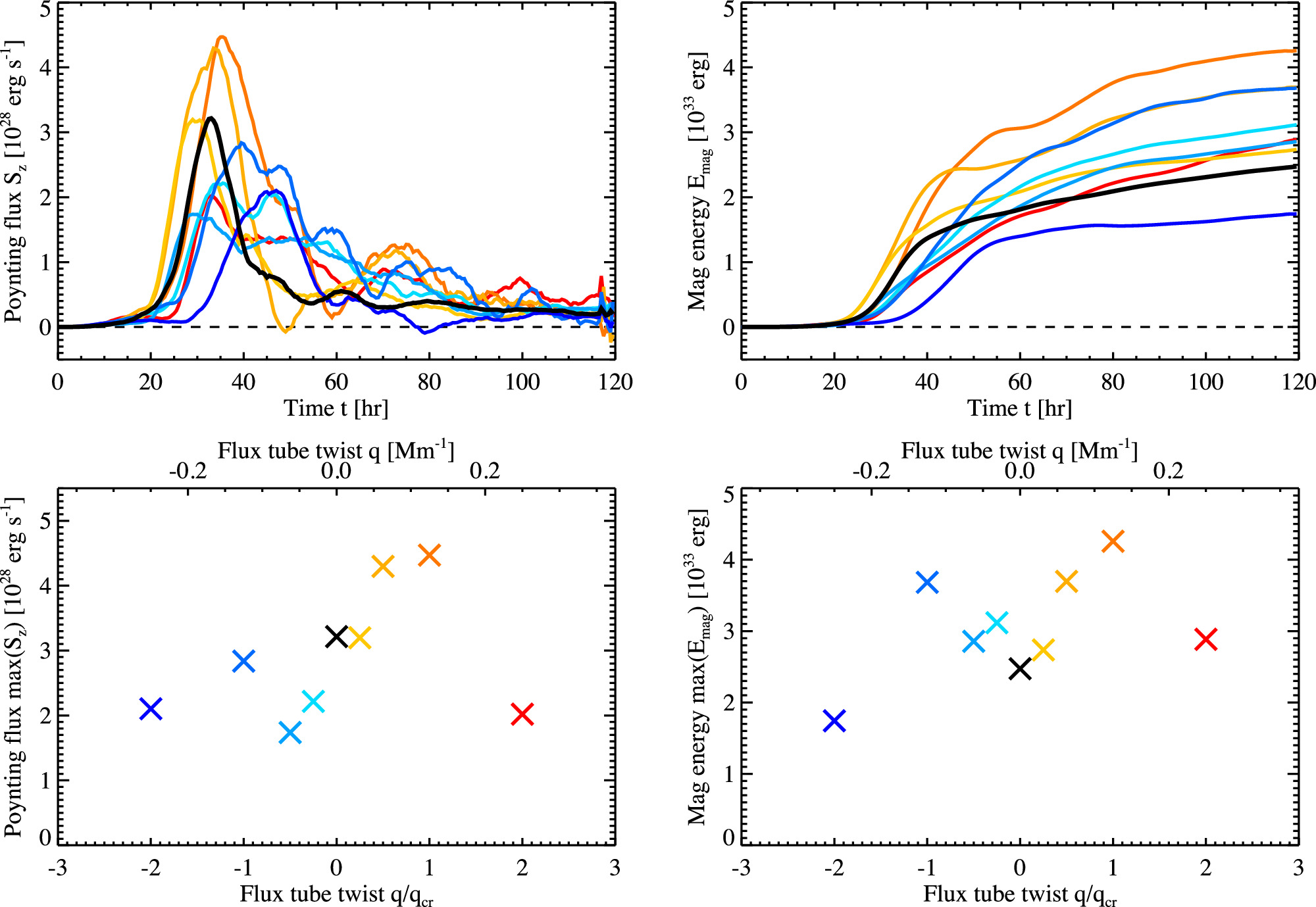
Results: Magnetic energy (Analysis)
- Peak Poynting flux ($max(S_z)$) and total injected energy ($max(E_{mag})$) are highest for intermediate twists ($|q/q_{cr}| = 1/2, 1$).
- The $q/q_{cr} = -1$ case has a relatively low $max(S_z)$ but large final $E_{mag}$ due to prolonged injection.
- For extreme twists ($|q/q_{cr}| = 2$), $E_{mag}$ is low because flux emergence is less successful (lower $\Phi_{max}$).
Discussion & Conclusion
Key findings summarized
- Magnetic flux emergence: Flux tubes rise via convective upflows, even without initial twist. However, sufficient twist is needed to maintain integrity against shredding and allow significant flux to reach the photosphere.
- Magnetic twist: Photospheric twist ($\alpha_{av}$) reflects the initial tube twist ($q$), but saturates at high initial twists. Values generally remain within realistic observational ranges.
- Magnetic helicity: Convection injects helicity even into untwisted tubes. Initial twists at or above the kink threshold ($|q/q_{cr}| \geq 1$) produce normalized helicity values much larger than observed in typical or even super-flaring ARs.
Theoretical implications
- $\delta\text{-}$Spot Formation: Given the unrealistic helicity injection for kink-unstable tubes ($|q/q_{cr}| \geq 1$), kink instability (triggered by excessive initial twist) might not be the primary mechanism for forming highly flare-productive $\delta$-spots under realistic convective conditions. Alternative mechanisms (e.g., interactions between multiple flux tubes) warrant further investigation.
- Role of convection: Convection is crucial for both driving emergence (even for non-buoyant tubes) and modifying helicity. It also highlights the importance of initial twist for flux tube survival.
- Magnetic energy transport: Only a small fraction (<10%) of the initial magnetic energy stored deep below ($E_{mag, init}$) is successfully transported into the upper atmosphere as Poynting flux ($E_{mag}$). Most energy remains within the convection zone.
Limitations and future work
- Study Limitations:
- Difficult to definitively confirm or rule out kink instability occurrence deep within the turbulent convection zone.
- Results might depend on the initial depth and specific location of the flux tube.
- Future Directions:
- Explore a wider parameter space (initial depth, field strength, radius).
- Simulate alternative $\delta$-spot formation mechanisms incorporating convection.
Questions?
Thank you for listening!
참고 문헌
- Toriumi, S., 2024, Convective Magnetic Flux Emergence Simulations from the Deep Solar Interior to the Photosphere: Comprehensive Study of Flux Tube Twist, Astrophysical Journal