Numerical Methods for MHD - Part 1: Introduction and Basic Equations

Series Navigation

• Part 1: Introduction and Basic Equations
• Part 2: Numerical Methods and Solution Techniques
• Part 3: Riemann Solvers
• Part 4: Advanced Topics

Numerical Methods for MHD Equations

Donghui Son
School of Space Research, Kyunghee University
October 3rd, 2024
Solar Dynamics Laboratory

Solar Dynamics Lab (Prof. Tetsuya Magara)

Shock wave produced by emerging flux

Solar penumbral microjet

Flux emergence

Research Focus

• Conducting advanced numerical simulations to investigate complex solar phenomena
• Utilizing state-of-the-art computational resources, including a high-performance local cluster capable of parallel processing with 512 cores
• Developing and applying sophisticated MHD models to study solar interior and solar exterior

Objectives

1. Understand the fundamentals of Magnetohydrodynamics (MHD).
2. Learn finite difference and finite volume methods for solving MHD equations.
3. Handle discontinuous solutions (shocks, contact discontinuities) in MHD simulations.

Table of Contents

1. Introduction to MHD
2. MHD Equations and Their Properties

---

1. Introduction to MHD

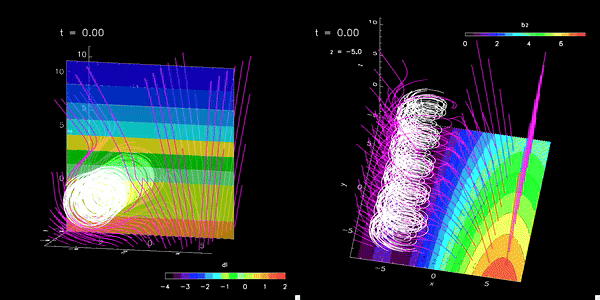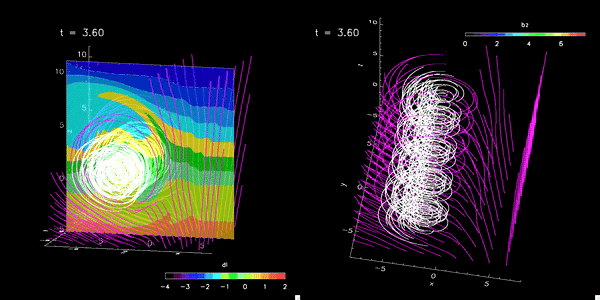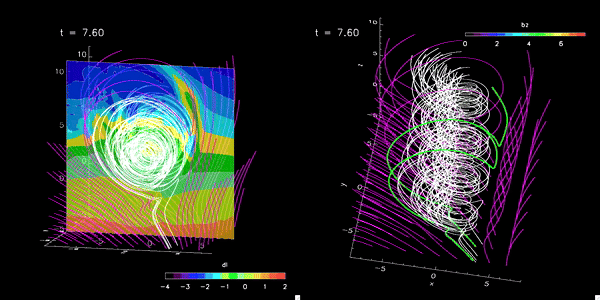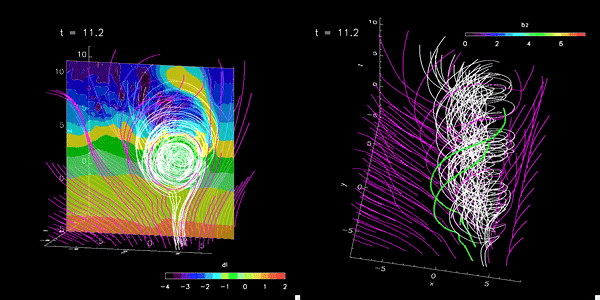
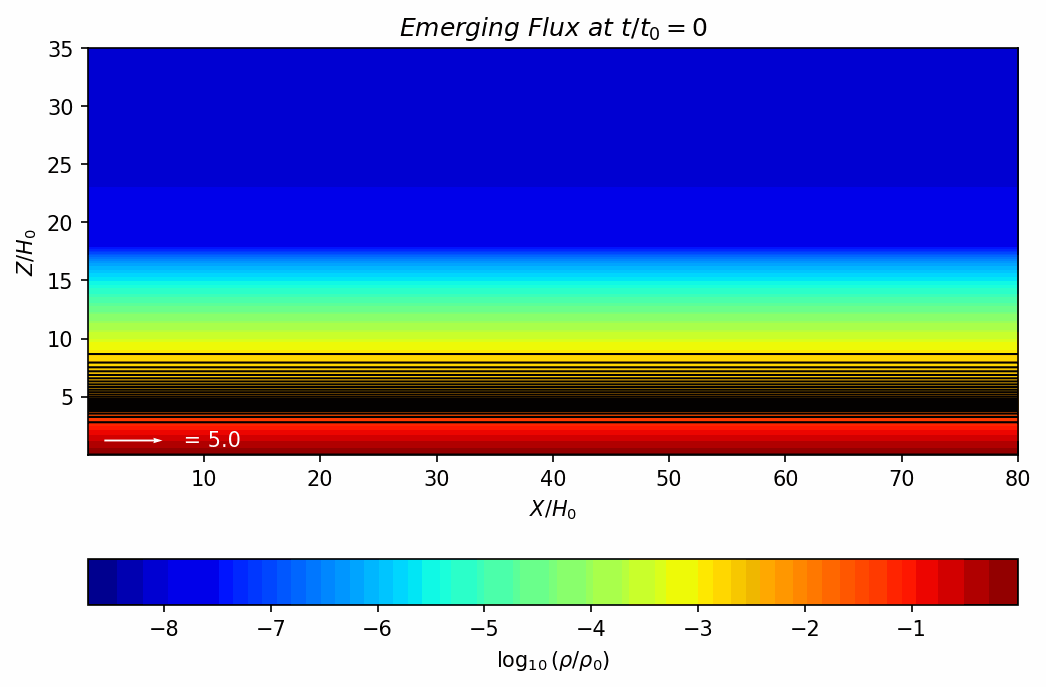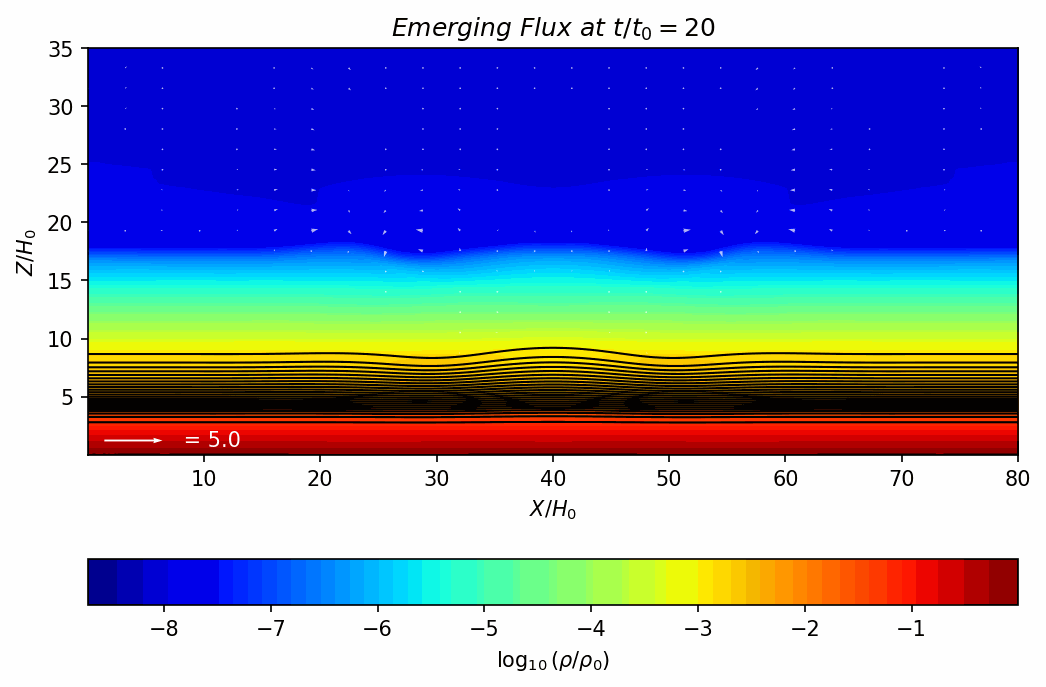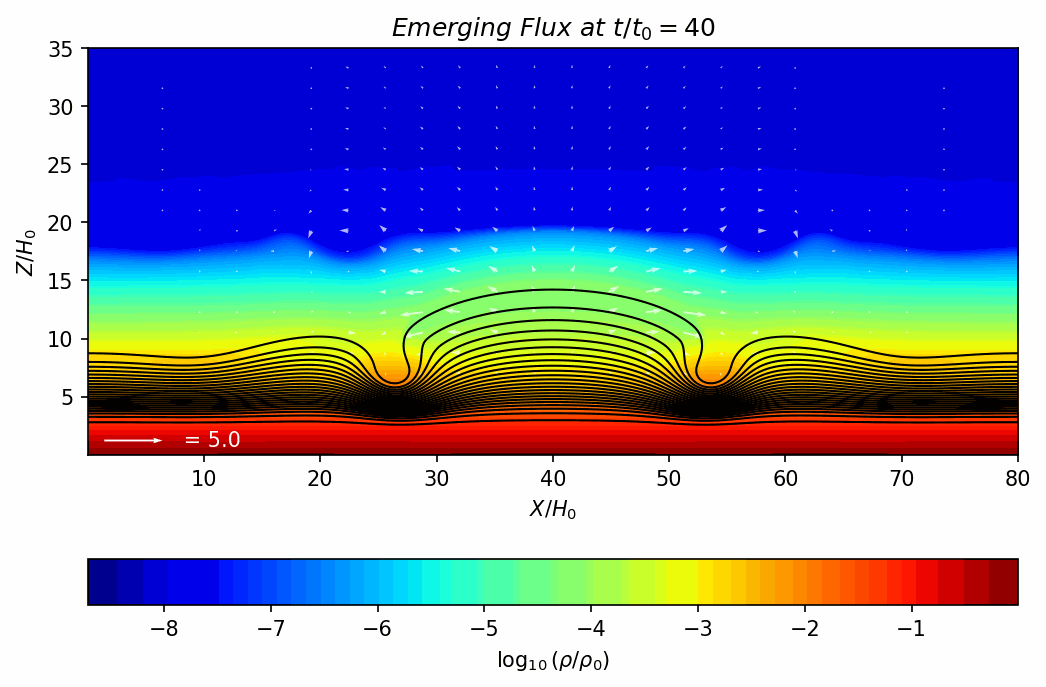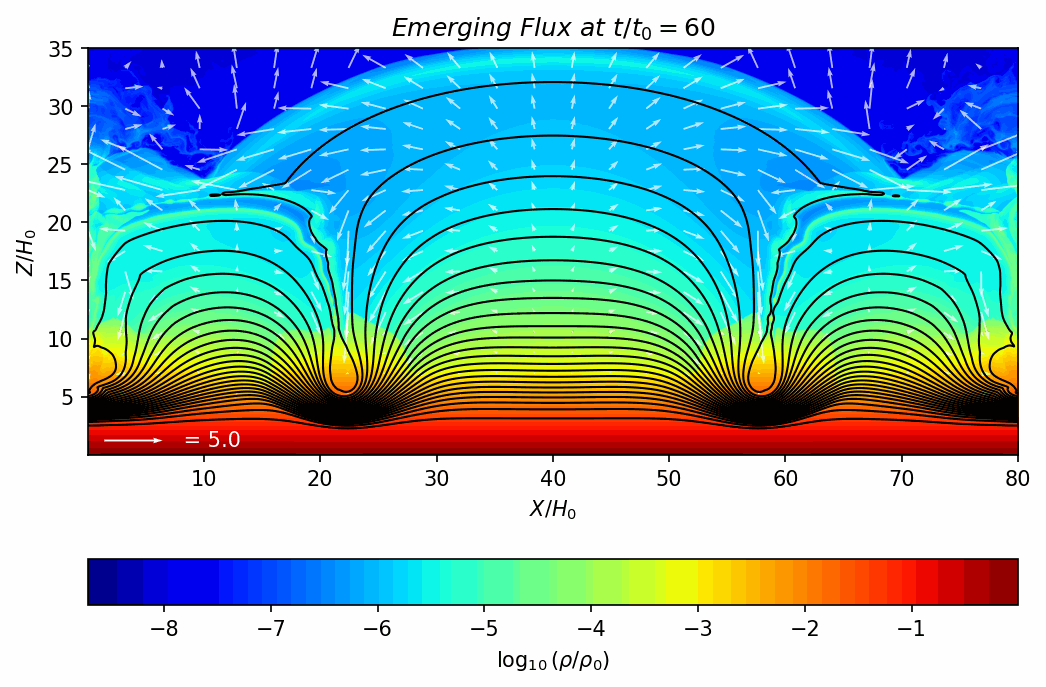
Magnetohydrodynamics (MHD) combines fluid dynamics and electromagnetism to describe the motion of a conducting fluid in a magnetic field. MHD appears in many contexts, including solar flares, fusion reactors, astrophysical jets, and more. Discontinuities (such as shocks and current sheets) are common in these high-energy plasmas, which require robust numerical methods to capture accurately.

2. MHD Equations and Their Properties

2.1 Basic Equations

In ideal MHD, we typically write the governing equations in conservative form to facilitate numerical methods (especially finite volume methods). The system involves mass, momentum, and energy conservation, along with Maxwell’s equations simplified for a perfectly conducting fluid and non-relativistic speeds.

1. Continuity (Mass Conservation):

   \[\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{v}) = 0.\]

   This equation ensures total mass is conserved in the fluid. Here, $\rho$ is the mass density, and $\mathbf{v}$ is the fluid velocity field.

2. Momentum Conservation:

   Rather than using the material derivative explicitly, we express momentum conservation in a divergence form:

   \[\frac{\partial (\rho \mathbf{v})}{\partial t} + \nabla \cdot (\rho \mathbf{v} \otimes \mathbf{v} + p \mathbf{I} - \frac{1}{\mu_0} \mathbf{B} \otimes \mathbf{B}) = 0,\]

   where

   • $p$ : Thermal pressure,
   • $\mathbf{I}$ : Identity matrix,
   • $\mathbf{B}$ : Magnetic field,
   • $\mu_0$ : Vacuum permeability,
   • $\otimes$ : Outer product (tensor product) operator.

   This form encapsulates the Lorentz force $\mathbf{J} \times \mathbf{B}$ by noting that $\nabla \cdot (\mathbf{B} \otimes \mathbf{B}) = \mathbf{B} \cdot (\nabla \cdot \mathbf{B}) - \nabla \times (\nabla \times \mathbf{B})$ when $\nabla \cdot \mathbf{B} = 0$.

   Note: In some treatments, momentum conservation is written as $\rho \frac{D \mathbf{v}}{D t} = -\nabla p + \mathbf{J} \times \mathbf{B}$, using the material derivative $D/Dt$. Numerically, however, the Eulerian (divergence) form is more common in finite volume solvers.

   • Eulerian vs. Lagrangian Derivatives:

     • Eulerian (fixed point in space):

       \[\frac{\partial \mathbf{v}}{\partial t},\]

     • Lagrangian (following fluid particle): \(\frac{D \mathbf{v}}{D t}.\)

3. Energy conservation

   We define the total energy density $e$ to include internal, kinetic, and magnetic contributions:

   \[e = \left( \frac{p}{\gamma - 1} + \frac{1}{2} \rho ||\mathbf{v}||^2 + \frac{||\mathbf{B}||^2}{2\mu_0} \right).\]

   The corresponding conservation law in divergence form is:

   \[\frac{\partial e}{\partial t} + \nabla \cdot \Bigg[\Big(e + p + \frac{||\mathbf{B}||^2}{2\mu_0}\Big)\mathbf{v} - \frac{(\mathbf{v}\cdot\mathbf{B})\mathbf{B}}{\mu_0}\Bigg] = 0.\]

   Here, $p = (\gamma - 1)(e - \frac{1}{2} \rho ||\mathbf{v}||^{2} - \frac{||\mathbf{B}||^{2}}{2\mu_0})$ is the thermal pressure, with $\gamma$ as the adiabatic index.

4. Magnetic induction equation

   Under the assumption of infinite conductivity (ideal MHD), the magnetic field evolves according to:

   \[\frac{\partial \mathbf{B}}{\partial t} + \nabla \cdot (\mathbf{v} \otimes \mathbf{B} - \mathbf{B} \otimes \mathbf{v}) = 0,\]

   which is equivalent to:

   \[\frac{\partial \mathbf{B}}{\partial t} = \nabla \times (\mathbf{v} \times \mathbf{B}).\]

5. Divergence-free condition

   This enforces that magnetic monopoles do not exist and that the net flux of $\mathbf{B}$ through any closed surface is zero:

   \[\nabla \cdot \mathbf{B} = 0.\]

2.2 MHD Wave Modes

In MHD, the coupling between the fluid flow and the magnetic field gives rise to several distinct wave modes. Below are the main categories and their key properties.

1. Alfvén Waves

   • Alfvén Speed:

     \[v_A = \frac{B}{\sqrt{\mu_0 \rho}}.\]

   • Characteristics:

     • Transverse, incompressible waves (fluid displacement is perpendicular to both the magnetic field and the direction of propagation).
     • Magnetic tension ($\mathbf{B}$-line tension) acts as the restoring force.
     • Propagate along magnetic field lines without changing the pressure or density significantly.

2. Magnetosonic Waves

   Because these waves involve both fluid pressure and magnetic field, we refer to them as “magnetosonic.” They can be further divided into fast and slow modes, depending on how they propagate relative to the magnetic field lines.

• Fast Magnetosonic Waves

  • Speed:

    \[c_{fast} = \sqrt{\frac{1}{2} \left( c_s^2 + v_A^2 + \sqrt{(c_s^2 + v_A^2)^2 - 4 c_s^2 v_{A}^2 \cos^2 \theta}\right)},\]

    where $c_s = \sqrt{\frac{\gamma p}{\rho}}$ is the sound speed and $v_A$ is the Alfvén speed. The $\theta$ is the angle between the wave propagation direction and the magnetic field.

  • Characteristics:

    • Compressible waves involving both magnetic and gas pressures.
    • Can propagate in any direction relative to the magnetic field.
    • Typically the fastest MHD wave mode for most angles $\theta$.
    • Behave like a combination of standard sound waves and Alfvén waves.

• Slow Magnetosonic Waves

  • Speed:

    \[c_{slow} = \sqrt{\frac{1}{2} \left( c_s^2 + v_A^2 - \sqrt{(c_s^2 + v_A^2)^2 - 4 c_s^2 v_{A}^2 \cos^2 \theta} \right)}.\]

  • Characteristics:

    • Compressible, but typically propagate slower than the fast mode, especially for non-zero $\theta$.
    • Strongly influenced by both magnetic tension and gas pressure.
    • Tend to move more “along” field lines, especially in low-$\beta$ plasmas (where magnetic pressure dominates).
    • Represent the slowest of the MHD wave families (apart from purely static modes).

2.3 Compact Form

A more compact way to write the MHD system:

\[\frac{\partial U}{\partial t} + \nabla \cdot \mathbf{F}(U) = 0.\]

• Conserved Variables $U$:

  \[U = \begin{pmatrix} \rho \\ \rho \mathbf{v} \\ e \\ \mathbf{B} \end{pmatrix}.\]

• Flux Function $\mathbf{F}(U)$: \(\mathbf{F}(U) = \begin{pmatrix} \rho \mathbf{v} \\ \rho \mathbf{v} \otimes \mathbf{v} + \left( p + \frac{B^2}{2\mu_0} \right) \mathbf{I} - \frac{1}{\mu_0} \mathbf{B} \otimes \mathbf{B} \\ \left( e + p + \frac{B^2}{2\mu_0} \right) \mathbf{v} - \frac{(\mathbf{v} \cdot \mathbf{B}) \mathbf{B}}{\mu_0} \\ \mathbf{v} \otimes \mathbf{B} - \mathbf{B} \otimes \mathbf{v} \end{pmatrix},\)

where:

• Terms in $\mathbf{F}(U)$ represent mass, momentum, energy, and magnetic fluxes in the $x$, $y$, and $z$ directions.